Leonard Ojler (Leonhard Euler) rođen je 15. aprila 1707. godine u Bazelu, kao prvo dete svojih roditelja Pola (Paul) i Margarite (Margaretha). Pol Ojler bio je sveštenik Reformatorske crkve, a majka je, takođe, poticala iz svešteničke porodice. Ubrzo nakon Ojlerovog rođenja porodica se preselila u Rien. Pol Ojler bio je prijatelj sa poznatom porodicom matematičara, Bernuli (Bernoulli), pa je Johan Bernuli (Johann Bernoulli), jedan od najznačajnijih evropskih matematičara toga vremena, izvršio značajan uticaj na mladog Ojlera.
Bio je veoma napredno dete. Već sa 13 godina upisao se na Univerzitet u Bazelu, a 1723. godine je i diplomirao sa radom, u kome je upoređivao Dekartovu (Descartes) i Njutnovu (Newton) filozofiju. U to vreme, Ojlerovi glavni predmeti bili su teologija, grčki i hebrejski jezik. Pol Ojler želeo je da njegov sin nastavi očevim stopama i postane sveštenik. Tada se umešao Johan Bernuli i uspeo da ubedi Ojlerove da je njihov sin predodređen da postane veliki matematičar.
Godine 1726. Ojler je završio svoju doktorsku tezu o širenju zvuka, pod nazivom “O zvuku”, a već naredne godine učestvovao je na takmičenju koje je organizovala Francuska akademija nauka. Tada je osvojio drugu nagradu, ali će kasnije tokom života osvojiti prvu nagradu na ovom prestižnom takmičenju čak 12 puta.

Portret Leonarda Ojlera, jednog od najznačajnijih matematičara u istoriji ove nauke
Na početku svoje naučne karijere Ojler dobija ponudu od Bernulijevog sina da mu se pridruži na Carskoj ruskoj akademiji nauka u Sankt Peterburgu. Ojler prihvata tu ponudu i u rusku prestonicu stiže 17. maja 1727. godine. Počinje da radi u matematičkom odseku Akademije, a pored toga, radi i kao lekar u ruskoj mornarici. Ojler je brzo napredovao i već 1731. godine postavljen je za profesora fizike. Dve godine kasnije, Danijel Bernuli (Daniel Bernoulli) odlučuje da se vrati u Bazel, a Ojler zauzima njegovo mesto na čelu katedre za matematiku. U to vreme Ojler počinje sa radom na geografskim kartama, da bi se 1740. godine povukao i prestao da se bavi kartografijom.
Ojler se oženio Katarinom Gsel (Katharina Gsell), kćerkom slikara koga je Petar Veliki (Pёtr I Alekseevič; Pёtr Velikiй) doveo u svoju službu iz Holandije. Ojler je sa svojom suprugom živeo u kući na obali reke Neve. Imali su 13 dece, od kojih je osmoro umrlo još u detinjstvu.
Zbog stalnih nemira u Rusiji toga vremena, prihvata ponudu Fridriha Velikog (Friedrich dem Großen) i 1741. godine prelazi na Berlinsku akademiju nauka. Sledećih 25 godina života proveo je u Berlinu. Bio je šef odseka za matematiku, a rešavao je i najrazličitije probleme Akademije, kao što su finansijski proračuni, objavljivanje naučnih radova, a bio je i državni savetnik za igre na sreću, osiguranja i penzione fondove. U ovom periodu Ojler je napisao preko 380 matematičkih radova, među kojima su i njegova dva najznačajnija dela “Uvod u analizu beskonačnih veličina” iz 1748. godine i “Diferencijalni račun” iz 1755. godine.
Jedan od zadataka koje je Fridrih Veliki postavio Ojleru bio je da podučava njegovu rođaku, princezu od Anhalt-Desaua (Anhalt-Dessau). Tokom 1760. i 1761. godine Ojler je sa princezom razmenio preko 200 pisama. Pisma su kasnije sakupljena i objavljena u knjizi pod nazivom “Pisma jednoj nemačkoj princezi”. U njima se Ojler uglavnom bavio izlaganjem fizičkih i matematičkih problema. Knjiga je postala veoma popularna širom Evrope i Amerike, što je dokaz da je Ojler imao sposobnost uspešnog predstavljanja naučnih tema širokoj publici.
Posle sukoba koje je imao sa Fridrihom Velikim, kao i Volterom (Voltaire), jednim od vodećih filozofa na Akademiji, Ojler je odlučio da napusti pruski dvor i Akademiju.
Njegov vid se s godinama sve više pogoršavao. Još tokom svog prvog boravka u Rusiji, skoro potpuno je oslepeo na desno oko, a 1766. godine levo oko mu je obolelo od katarakte, što je za svega nekoliko nedelja dovelo do potpunog slepila. Međutim, to nije uticalo na Ojlerov rad. Imao je izvanredno pamćenje i mogao je da vrši veoma složene proračune u glavi. Pisanje je zamenio diktiranjem, ali se broj radova koje je objavljivao nije smanjio.
Ojler se bavio različitim oblastima matematike, a njegov doprinos ovoj nauci veoma je značajan. U matematičku notaciju uveo je pojam funkcije i prvi je sa f(x) obeležio funkciju po promenljivoj iks. Osim toga, uveo je moderan zapis trigonometrijskih funkcija, slovo e – kao oznaku za osnovu prirodnog logaritma (danas poznatije kao Ojlerov broj), veliko grčko slovo sigma – za označavanje sumiranja i slovo i – za označavanje imaginarne jedinice. Sve ove oznake se i danas koriste u matematici.
Porodica Bernuli imala je značajan uticaj na Ojlerov rad. Oni su važili za najznačajnije matematičare 18. veka, koji su se bavili matematičkom analizom, a svoje interesovanje za ovu oblast preneli su i na Ojlera. Njegov najveći doprinos bio je u oblasti stepenih redova. Počeo je i da upotrebljava eksponencijalne funkcije i logaritme u analitičkim dokazima. On je takođe definisao i eksponencijalnu funkciju za kompleksne brojeve i otkrio njenu vezu sa trigonometrijskim funkcijama. Veza između ovih funkcija dobila je naziv Ojlerova formula. Poseban slučaj te formule dobija se kada je ugao jednak π i poznat je pod nazivom Ojlerov identitet. Ojlerov identitet je, prema mišljenju mnogih matematičara, jedna od najznačajnijih matematičkih formula zato što se u jednom izrazu, uz korišćenje operacija sabiranja, množenja i stepenovanja navodi pet važnih matematičkih konstanti 0, 1, e, i, π. Zanimljivo je da je upravo ovaj identitet 1988. godine proglašen za najlepšu matematičku formulu svih vremena.
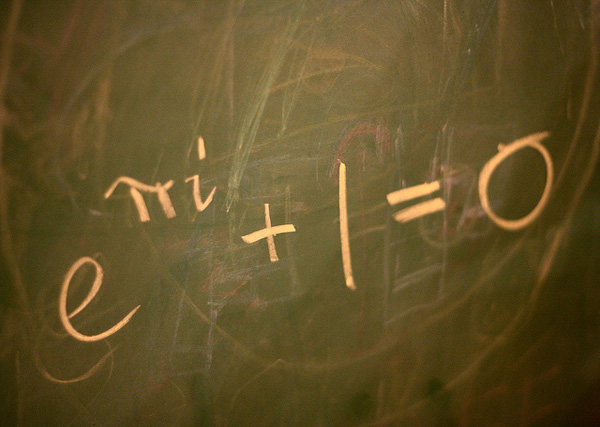
Ojlerov identitet proglašen je najlepšom matematičkom formulom
Ojler je imao značajnog uticaja i u razvoju moderne kompleksne analize, a smatra se i jednim od osnivača teorije brojeva. Bavio se i analitičkom geometrijom i formulisao je jednačine koje opisuju različite rotacione površi.
Tokom svog prvog boravka u Rusiji, 1736. godine, rešio je poznati problem Kenizberških mostova. Naime, glavni grad Pruske, Kenigzberg, nalazi se na reci i njegova teritorija obuhvata dva velika ostrva koja su povezana, sa ostatkom grada i međusobno, pomoću sedam mostova. Pitanje je bilo da li je moguće poći iz jedne tačke i vratiti se u nju, tako da se svaki most pređe tačno jedanput. Ojler je dokazao da to nije moguće, odnosno da ne postoji Ojlerov put. Ovo rešenje se smatra prvom teoremom teorije grafova, koja danas ima ogromnu primenu u modernim naukama.
Godine 1766. prihvatio je poziv da se vrati na Peterburšku akademiju. Pet godina posle dolaska u Rusiju, u Ojlerovoj kući izbio je požar. Preživeo je zahvaljujući svom vernom slugi, koji je uspeo da ga izvuče iz vatrom zahvaćene kuće. Međutim, nesreće su nastavile da se nižu, pa je pet godina kasnije Ojlerova supruga preminula. On se već sledeće godine ponovo oženio i to Katarininom polusestrom Salome Abigajl Gsel (Salome Abigail Gsell).
Umro je 18. septembra 1783. godine u Sankt Peterburgu, nakon što je doživeo moždani udar. Bio je sahranjen pored svoje prve žene na luteranskom groblju na ostrvu Vasiljevski. Ovo groblje je kasnije uništeno, a Ojlerovi ostaci preneseni su u pravoslavni manastir Aleksandra Nevskog u Sankt Peterburgu.
Izvor fotografija: wikipedia.org, flickr.com
Prethodne tekstove iz serijala “Ljudi koji su pomerali granice” možete pronaći ovde.
Jovana Filipović je studentkinja Elektrotehničkog fakulteta, perfekcionista, namćor i statista sreće kao iz Balaševićevih pesama u čijim se stihovima pronalazi. Pevam svoj blues bez namere bitne, za zlo sam teški laik, i možda i nisam neki biser, ali sam barem svoj režiser. A kao omiljeni stih i moto izdvajam: “Brojao sam ljude s krsta, pravila i izuzetke. Posvud promašena vrsta, samo retki nađu retke.”
















